Giovanni Francesco Zarbula

Tento malíř a tvůrce slunečních hodin z Piedmontu, nám zanechal úžasné dědictví lidového umění ve vesnicích francouzských Alp. V letech 1832 až 1870 vytvořil téměř stovku slunečních hodin v oblasti mezi Grenoblem a Gapem, v blízkosti italských hranic. Více než polovinu těchto bohatě zdobených a skvěle výtvarně provedených děl je stále možno nalézt na stěnách domů v této oblasti, mnohé z nich byly navíc v poslední době odborně zrestaurovány.
Je úžasné, jak tento kočovný umělec, cestující po kraji na oslu a jehož pomocnými nástroji byly toliko kolík a špagát, dokázal navrhnout a zrealizovat takové množství slunečních hodin. Je dokonce zajímavé, že Zarbula při konstrukci svých slunečních hodin neměřil ani azimut stěny, i když jsou většinou orientované na jinou stranu než přesně na jih. On to zkrátka nepotřeboval. Podle některých stop nalezených na číselnících se zdá, že Zarbula aplikoval variantu "indických kruhů", jejichž pomocí vytýčil na zdi přímku pro rovnodennost a substylos. Díky tomu pak mohl s použitím znalostí geometrických a gnómických pravidel vynést jednotlivé hodinové rysky.
Vlastním rozborem Zarbulovy metody se podrobně zabýval Paul Gagnaire. Jeho poznatky byly zahrnuty ve velice zdařilé presentaci z roku 2005 jejíž autory jsou Roger Bailey a Alain Ferreira (1), kterým tímto děkuji za svolení použít jejich snímky. Na základě jejich materiálu byl vypracován také tento článek. Technikou určení polohy ukazatele se zabýval také Michel Ugon, který zpřesnil postup celé metody. Fenomén těchto slunečních hodin se projevuje také na mnohých dílech z posledních let, jenž nesou neklamné znaky používané samotným Zarbulou před více než stotřiceti lety.

Charakteristické prvky

• Žádné hodiny nejsou na stěně natočené k severu (SV, SZ)
• Datová čára pro rovnodennost, která je využívaná při vlastní konstrukci
• Rysky pro celé hodiny ve tvaru šípu směřujícího od středu
• Používá polos - neboli šikmý ukazatel, který je rovnoběžný se zemskou osou
• Ptáci a květiny, kterými se odvolával na svůj vztah k přírodě
• Rám, závěsy a střapce jako znaky italského barokního umění
• Symbol Slunce a srpku Měsíce jako symbol dne a noci
• Zednářské a náboženské symboly
• Motto: Latinsky, francouzsky, italsky nebo provensálsky
• Signatura: GFZ nebo ZGF
• Datování pro období let 1830 - 1876

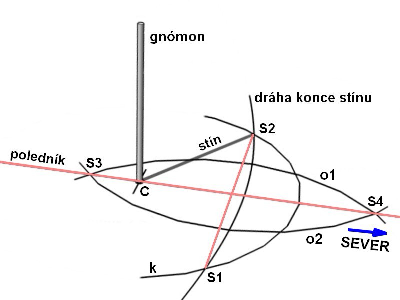
Metoda "Indických kruhů" je vcelku jednoduchá technika k nalezení severu pomocí Slunce. Tato metoda je přičítána Dšou Gungovi, jenž žil ve 12. století před naším letopočtem. Její princip vycházející z poznatku, že denní dráhy nebeských těles jsou souměrné vzhledem k poledníku. My si ji připomeneme v typické aplikaci na vodorovné ploše (zemi) viz obr. 1. Jediné pomůcky, které potřebujeme jsou kolík zapuštěný kolmo do země (gnómon), provaz k narýsováni kružnice k se středem v patě gnómonu C a Slunce. Sledováním pohybu stínu vrcholu gnómonu, zjistíme, že se pohybuje po hyperbole, která ve dvou místech S1 a S2 protne narýsovanou kružnici. Tyto dva průsečíky určují úsečku a leží přesně ve směru východ západ. Za pomocí provazu narýsujeme dva oblouky o1 a o2 o stejném poloměru se středy v bodech S1 a S2 tak, aby se protkly vně kružnice v bodě S4 . Spojením tohoto bodu se středem kružnice získáme osu souměrnosti úsečky S1S2 a také hyperboly. Tato osa, která je ve směru sever - jih je místní poledník.
Na těchto základech je založena Zarbulova metoda, když považoval svislý číselník slunečních hodin za ekvivalentní horizontálnímu někde jinde na Zemi.
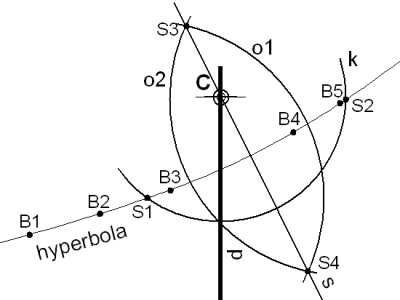
Připomeňme si, vše co používal byla svislá stěna natočená vzhledem k světovým stranám pod obecným úhlem, kolík, upevněný kolmo ke zdi, motouz a tužku. Sledováním pohybu konce stínu ukazatele během dne získal několik bodů, které proložil hyperbolou (ve dni rovnodennosti přímkou). Opsal oblouk se středem v patě ukazatele, který ve dvou místech protnul hyperbolu. Těmito dvěma body proložil úsečku, která je rovnoběžná s rovníkem a tedy i datovou čárou pro rovnodennost, jenž je vždy jako přímka. Tato velice důležitá čára je dobře viditelná na mnohých číselnících od Zarbuly viz odkaz 3. Konstrukcí osy souměrnosti k této úsečce získal směr substylu, nebo-li průmětu šikmého ukazatele (polosu) do roviny stěny. Polos je rovnoběžný s polární osou, takže svírá s polední přímkou doplňkový úhel zeměpisné šířky do 90°. Jak prosté.

Konstrukce hodin dle Zarbulovy metody

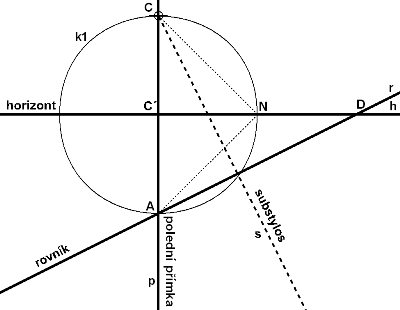
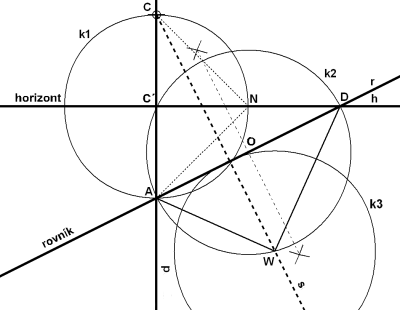
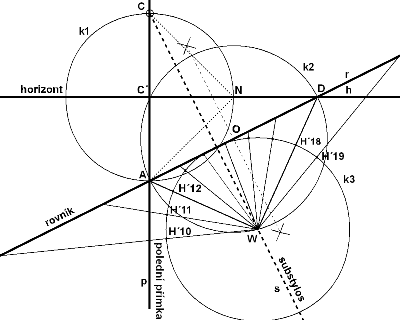
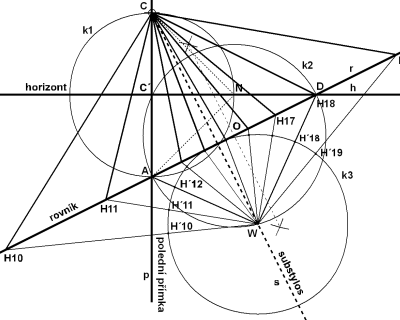
Použití této jednoduché metody bylo umožněno hlavně díky tomu, že jednotlivé lokality, ve kterých se Zarbulovy sluneční hodiny nacházejí, jsou v okolí 45 rovnoběžky. V závislosti na této skutečnosti, úhly, se kterými při konstrukci pracujeme mají 90, 45 a 15 stupňů a tak při konstrukci opravdu vystačíme toliko s tužkou, pravítkem a kružítkem a samozřejmě Sluncem. A to je vlastně to samé, s čím pracoval Zarbula. Na stěně vyznačíme bod pro patu ukazatele a označíme jako C. V tomto místě zapustíme kolmo ke zdi tyčku s ostrým hrotem. Z bodu C spustíme svisle dolů polední přímku p. Během slunečného dne sledujeme pohyb konce stínu a průběžně děláme značky (B1, B2, B3, B4, B5), které poté proložíme hyperbolou. Narýsujeme oblouk k se středem v C, tak aby protnul námi vytvořenou křivku ve dvou bodech (S1, S2). Úsečka proložená těmito body je rovnoběžná s rovinou rovníku. Pomocí oblouků o stejném poloměru (o1, o2) opsaných kolem bodů S1 a S2 vzniknou průsečíky S3 a S4 jenž leží s bodem C v ose souměrnost hyperboly. Tuto osu nazýváme substylos - viz obr. 2. Dále vyneseme vodorovnou čáru pro horizont, která je kolmá na polední přímku a tuto protíná v přiměřené vzdálenosti pod bodem C kde vznikne bod C´. Se středem v bodě C´ opíšeme kružnici k1 o poloměru CC´. Tato kružnice nám vyznačí bod A na polední přímce p a bod N na horizontální čáře h. Bod N označuje polohu nodu sklopeného do roviny stěny, pokud se jej rozhodneme použít. Spojnice bodů C a N zase znázorňuje polos sklopený do roviny stěny viz obr. 3. jehož pata se nachází v bodě C. Úhel mezi polosem a polední přímkou se rovná doplňkovému úhlu zeměpisné šířky, zde 45°. Bodem A proložíme přímku kolmou na substylos s. V místě, kde protne přímku horizontu, vznikne bod D označující 6. případně 18. hodinu (H6 nebo H18) v závislosti na tom, zda je zeď natočena k východu či k západu. Na stěně orientované přesně na jih, je polední přímka totožná se substylem, rovníková přímka rovnoběžná s horizontem a bod D vychází v nekonečnu. Rozpůlením úsečky AD na rovníkové přímce získáme střed O pomocné kružnice k2 - viz obr. 4. V místě průsečíku kružnice k2 s přímkou s vznikne bod W, což bude vrchol pravoúhlého trojúhelníku AWD, který leží v rovině rovníku a my jsme ho tak otočily do roviny stěny. Dalším důležitým pravidlem je, že rameno 6. a 12. hodiny svírá v rovině rovníku úhel 90°, zde je to úhel AWD=90°. Opíšeme kružnici k3 se středem v bodu W. Tuto kružnici můžeme chápat jako číselník rovníkových slunečních hodin, který je sklopený do roviny stěny. Kružnici tedy rozdělíme po 15. stupních (360° = 24 hodin a tedy 15° = 1 hodina) vzhledem k ramenům trojúhelníku AWD (body H´1…n) - viz obr. 5. Jednotlivými body H´ vedeme z bodu W přímky až na rovníkovou přímku (body H1…n), kde získáme polohy jednotlivých hodinových značek. Teď již můžeme vyznačit jednotlivé hodinové čáry. Uděláme to tak, že bodem C protáhneme přímky k jednotlivým hodinovým značkám H na rovníkové přímce - viz obr. 6.

Tímto způsobem jsem si ověřil přesnost a funkčnost této metody s využitím základních rýsovacích pomůcek. O správnosti této metody mne ujistily také dobře znatelné stopy vlastní konstrukce na některých Zarbulových číselnících (3). Kontrolu přesnosti jsem provedl na číselníku, který jsem vygeneroval pomocí programu Orologi Solari (http://digilander.libero.it/orologi.solari/) pro 45 rovnoběžku s azimutem stěny 30°. Jak jsem uvedl již dříve, Zarbula pracoval v okolí 45. rovnoběžky. To má velký význam, jelikož to zjednodušuje vlastní konstrukci, při které si opravdu vystačíme jenom s tužkou, kolíkem a provazem. Když jsem ale chtěl provést konstrukci číselníku touto metodou pro 51. rovnoběžku, musel jsem použít navíc úhloměr, abych dospěl ke správnému řešení.

Přílohy:

Zdroje:

Jaromír Ciesla, listopad 2009